
Resumen
En la actualidad, la sociedad considera que la investigación tiene que ir enfocada a una aplicación concreta, sin embargo, esto no tiene por qué ser siempre así. En el siguiente trabajo se ha realizado una investigación sobre varios casos, en los cuales la investigación sobre temas irrelevantes en matemáticas muchas veces deriva en resultados inesperados y de gran utilidad. Las cosas no tienen que "servir" para algo en este momento para que tengan relevancia en el futuro. Dentro de esta amplia premisa, el proyecto se ha centrado principalmente en la teoría de números; junto a esto, se ha hecho una exposición de propiedades y curiosidades de diversos tipos de números, que muestran la potencial belleza que pueden llegar a tener las matemáticas y cómo estas son un arte como cualquier otro. Con este estudio, se ha podido concluir que la investigación en matemáticas, aunque a priori pueda parecer irrelevante, es posible que tenga aplicaciones sorprendentes para resolver problemas en el futuro. Además, se ha mostrado la belleza de las matemáticas mediante una gran cantidad de propiedades y curiosidades sobre los números antes mencionados.
Índice
1. Introducción
En el siguiente proyecto voy a exponer cómo la investigación en temas aparentemente irrelevantes en matemáticas, pueden tener suma importancia en el futuro, a pesar de que en el momento en el que se investiguen pueda parecer que no "sirven" para nada. Esto es algo importante a tener en cuenta, ya que, en la actualidad, prácticamente toda la investigación científica parece que tiene que estar dirigida hacia una aplicación concreta para poder llevarse a cabo. Sin embargo, a lo largo de la historia se ha podido comprobar en multitud de casos, cómo estudios o descubrimientos que en su momento no tenían aplicación alguna, han sido decisivos para otros avances en ciencia o tecnología en el futuro.
Como consecuencia, permítasenos decir que la investigación básica es -además de bella- útil, pero que no podemos saber cuándo surgirán sus aplicaciones en otros campos. En todo caso, lo que sí podemos asegurar es que la investigación que no se hace nunca será útil (Varona, 2014, p. 22-23).
En adición, independientemente de la aplicación que puedan o no tener las matemáticas, tienen otra "utilidad" más que respetable, y esta es su inherente belleza, al igual que una pieza de piano de Chopin, un cuadro de Velázquez o una estatua de Miguel Ángel; y es que las matemáticas (junto a muchas otras ciencias y campos, que no es cuestión de desmerecer), pueden ser increíblemente bellas si las estudiamos por el mero placer de descubrir las propiedades que esconden los números, las figuras geométricas, etc. Para mostrar esta belleza, se han estudiado las propiedades de diferentes tipos de números y se han realizado algunas demostraciones de dichas propiedades, como mostraremos más adelante.
2. Objetivos
- Indagar sobre cómo la investigación de temas aparentemente irrelevantes puede tener aplicaciones sorprendentes en el futuro.
- Mostrar la belleza oculta en las propiedades de algunos números y tipos de números que mucha gente no ve.
3. Metodología
Se ha realizado una revisión bibliográfica sobre aspectos generales de la teoría de números concretando en los siguientes números: números perfectos, amigos, felices, metálicos (especialmente el número áureo y con ello la sucesión de Fibonacci), el número ? y el número de Graham.
La búsqueda se ha realizado utilizando Google Scholar seleccionando los documentos, tanto en español como en inglés, que contenían información sobre los números citados, excluyendo aquellos que no se centraban en los mismos. La información obtenida se ha clasificado en diferentes apartados: números metálicos, número ?, números perfectos y número de Graham.
4. Desarrollo
Algunos ejemplos de situaciones donde investigaciones tuvieron aplicaciones inesperadas mucho después de ser realizadas son los siguientes:
La máxima cantidad de esferas con las que puede estar en contacto otra esfera sin solapamientos en tres dimensiones es 12, y esto tiene una aplicación simple y rápida, ¿cuál es la forma más práctica de apilar naranjas? Sin embargo, los matemáticos fueron un paso más allá en sus investigaciones, y se dedicaron a comprobar cuál era la mejor manera de "apilar naranjas" en 4 o más dimensiones, cosa que en principio no tiene ninguna aplicación lógica, dado que nos encontramos en 3 dimensiones, sin embargo, resulta que las señales de sonido por líneas telefónicas se podrían tratar como esferas en 8 dimensiones, y que este trabajo aparentemente irrelevante resultó ser extremadamente práctico para aprender a enviar la máxima cantidad de información en el menor espacio posible (Rowlett, 2011).
Otro ejemplo relevante es la invención de los cuaterniones por Hamilton en 1843. Estos eran un nuevo tipo de números que ampliaban los números complejos y que, aparentemente, "no servían" para nada, sin embargo, muchos años más tarde los matemáticos les encontraron una importante utilidad en el campo de la visión tridimensional en la tecnología, donde eclipsaba ampliamente a las matrices (Rowlett, 2011).
Como último ejemplo citaremos el famoso Último Teorema de Fermat, que tardó más de 300 años en demostrarse (se demostró en 1996), y que establece que no existe ningún trío de números que cumpla que la suma de dos de ellos elevados a una potencia n dé como resultado otro número elevado a la misma potencia n para n mayor o igual que tres, dicho de otra forma: an = bn + cn para n>2 no tiene soluciones enteras distintas de la trivial. Este resultado, si bien curioso, resulta carente totalmente de relevancia, sin embargo, todos los métodos que se han tenido que desarrollar para llegar a esta conclusión han resultado ser extremadamente útiles, mostrando que no es valioso únicamente el final, sí que el camino también puede ser extremadamente relevante en ocasiones (Rowlett, 2011).
Para mostrar la belleza inherente de las matemáticas, se van a estudiar los distintos números propuestos. Los primeros son los números perfectos, los cuales tienen la curiosa propiedad de que la suma de sus divisores da como resultado el propio número. Los números perfectos son de la forma 2n?1 (2n?1), siempre que 2n? 1 fuera primo, estos primos son los denominados primos de Mersenne, y para que un número de esa forma sea un primo de Mersenne, n debe ser como mínimo, número primo, puesto que si no fuera primo n=ab; a,b>1.
Por lo que 2n? 1 = (2a)b? 1.
Y dado que (2a)b ? 1 = (2a? 1) ((2a)b?1 + (2a)b?2+... +2a+ 1) podemos deducir que no sería primo, ya que sería el producto de dos números.
Paralelamente, todos los números que no son perfectos son divididos en dos clases, los abundantes y los deficientes. Los números abundantes son aquellos para los que la suma de sus divisores es mayor que el mismo número. Mientras que los deficientes, por contraparte, suman menos que el propio número.
Estrechamente relacionados con los números perfectos también están los números amigos, los cuales van en pareja, y la suma de sus divisores en vez de dar como resultado el propio número da como resultado el otro número, la pareja más conocida es la del 220 y el 284, y es que la suma de los divisores del 220 da como resultado 284, y viceversa. Sobra mencionar que las parejas de números amigos serán siempre un número abundante y uno deficiente.
Otro tipo de números de especial relevancia son los números felices, y estos son aquellos que, tras someterlos al test de felicidad, acaban terminando en 1. El Test de felicidad consiste en sumar repetidas veces los cuadrados de los dígitos de un número.
Por ejemplo, el 7
72 = 49 ? 42 + 92 = 16 + 81 = 97 ? 92 + 72 = 81 + 49 = 130
? 12 + 32 + 02 = 1 + 9 = 10 ? 12 + 02 = 1
Sin embargo, al probar con otro número, el 4 por ejemplo, vemos que terminamos en un bucle formado por los números 4, 16, 37, 58, 89, 145, 42, 20 y vuelve al 4. El bucle no tiene por qué partir de uno de los miembros del mismo, por ejemplo, al empezar con el 2. Y se puede demostrar que todos los números acaban o en 1 o en este bucle.
Por otra parte, los números metálicos, son la solución a las ecuaciones de la forma x2 ? px ? q = 0. Aunque aquí realmente sólo voy a mencionar los tres más conocidos: el número de bronce, el de plata y el de oro, las soluciones a x2 ? 3x ? 1 = 0, x2 ? 2x ? 1 = 0 y x2 ? x ? 1 = 0 respectivamente. Al resolver las ecuaciones nos acaba dando ( 3 + ?13 ) / 2, 1 + ?2 y ( 1 + ?5 ) / 2 cuyos valores numéricos son aproximadamente 3.3028, 2.4142 y 1.6180. Y es en este último en el que nos vamos a centrar, pues es el conocido número áureo, y ha fascinado históricamente al ser humano por diversos motivos, por ejemplo, su curiosa relación con la sucesión de Fibonacci, pues resulta que, al ir dividiendo los términos de la sucesión de Fibonacci, el número resultante se va aproximando cada vez más al número áureo, y es que resulta que para la sucesión de Fibonacci se da que:
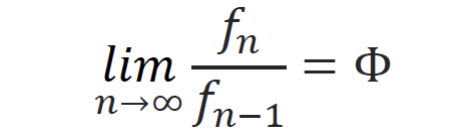
El ser humano ha basado muchísimas construcciones en el número áureo, siendo que podemos verlo en lugares como el Partenón, la pirámide de Keops, aparece mucho también en el arte del Renacimiento, como en la Mona Lisa o el Hombre de Vitruvio, y esto es normal, ya que el número áureo fascina al hombre desde siempre, sin embargo, resulta que este también aparece en la naturaleza, y es que la espiral de Durero, que se puede construir con la sucesión de Fibonacci, aparece en muchos sitios, en la propia naturaleza, como en la concha de un nautilus, en la forma de algunas galaxias, en tormentas, incluso en la disposición de hojas y pétalos de algunas plantas. Llegando incluso a aparecer en la propia geometría.
El número ? ha intentado ser aproximado por los matemáticos desde tiempos inmemoriales, es famoso esencialmente por su aparición en la fórmula del perímetro del círculo, en la que p=2r?, para p=perímetro y r=radio del círculo.
Los egipcios ya lo intentaron aproximar, y lo hicieron con bastante precisión. También aparece en La Biblia:
"Hizo el Mar de metal fundido, de diez codos de borde a borde. Era enteramente redondo y de cinco codos de alto. Un cordón de treinta codos medía su contorno." (2 Cr 4:2). Como se puede observar, en la Biblia se aproxima ? a 3.
Arquímedes lo consiguió aproximar de una manera muy interesante. Él construía polígonos regulares inscritos en el círculo y calculaba su perímetro. Por ejemplo, tomaba un pentágono, calculaba su perímetro p y, en proporción al radio r de la circunferencia, sacaba un valor aproximado de ?, cuantos más lados tenía el polígono, más se acercaba la proporción p/2r a ?. Lo llegó a hacer con un polígono de 96 lados.
En 1761, tras miles de años desde el "descubrimiento" de ?, Lambert consiguió demostrar que era irracional, y en 1882, Lindemann demostró también la trascendencia de ?, que implica que no es solución de ninguna ecuación algebraica, es decir, una ecuación en la que los coeficientes son números racionales.
Para finalizar, se expondrá el número de Graham, que es el número más grande que aparece en una demostración matemática. Siendo el resultado de una serie de cálculos. El número se construye mediante la flecha de Knuth, la cual funciona de la siguiente forma:
3?2 por ejemplo, significa 32, es decir, 9. Y así 2?4 es 24 que es 16.
Lo peculiar de la Flecha de Knuth es que se puede poner más de una flecha. Por ejemplo: 3??3, donde el número de la derecha indica el número de veces que aparece el número de la izquierda, separado de n-1 flechas, siendo n el número de flechas original. 3??3=3?3?3, y se empieza siempre por la derecha: 3?3?3=3?27=327=7 625 597 484 987. Como podemos, ver al añadir una flecha el número, aumenta rápidamente.
Para expresar el número de Graham, empezamos con esta base, 3????3, si la desarrollamos,
3???3???3=3???3??3??3=3???3??3?3?3 =3???3??7 625 597 484 987.
Este número es inconcebible, como se puede comprobar. Pues a este número lo vamos a llamar g1. Siendo g1 el número que se acaba de explicar, g2 resulta ser 3??...??3 donde el número de flechas entre los treses es, precisamente, g1, es decir que habría esa enorme cantidad de flechas entre un tres y otro. Si empezamos a desgajar, no sale una cadena de 3 gigantesca.
3?...g1-1...?3?...g1-2...?3?...g1-3. . .?3?. . .
Esa cadena g1 veces. Si llegáramos al final:
...?3????3???3??3?3?3=...?3????3???3??7 625 597 484 987
Obsérvese la parte subrayada, es g1, por lo que g2 es muy superior a g1. Se podrá deducir que g3 son dos treses separados de g2 flechas. Y este número no sólo es infinitamente superior a g2 si no que es infinitamente superior a lo ya superior que era g2 respecto a g1.
El número de Graham es g64.
5. Conclusiones
Con una gran cantidad de ejemplos, se ha podido mostrar cómo las matemáticas más teóricas y sin aparentes aplicaciones pueden llegar a tener utilidad en campos inimaginables; campos que no tenían ni por qué estar relacionados con las matemáticas o ni por qué haber existido en aquella época. Y que hoy en día las personas que piden que los matemáticos justifiquen la utilidad de sus investigaciones antes siquiera de hacerlas, son el equivalente adulto de los niños que hacen la típica pregunta de "¿Y, eso para qué sirve?".
También se han mostrado las propiedades de varios números, desde un punto de vista menos aplicado y simplemente más teórico, tratando de mostrar la belleza subyacente en las propiedades de estos números.
Bibliografía
Alonso, D. (2016). Números perfectos, multiperfectos y amigos. [Trabajo Fin de Grado, Universidad de Valladolid]. Uva http://uvadoc.uva.es/handle/10324/17209
Varona, J. L. (2014). Recorridos por la teoría de números. Electolibris.
García, L. (2011). Números notables. RBA.
Rowlett, P. (2011). The unplanned impact of mathematics. Nature, 475, 166-169

